Problém homogenity reakční směsi
Hydrogenace benzonitrilu vede k benzylaminu,
C6H5CN + 2H2 → C6H5CH2NH2
Tento průmyslový postup poskytuje rovněž, v malé míře, dibenzylamin jako vedlejší produkt. Trh někdy vyžaduje produkovat dibenzylamin ve větším množství. Vhodnou metodou je syntéza na základě benzaldehydu a benzylaminu:
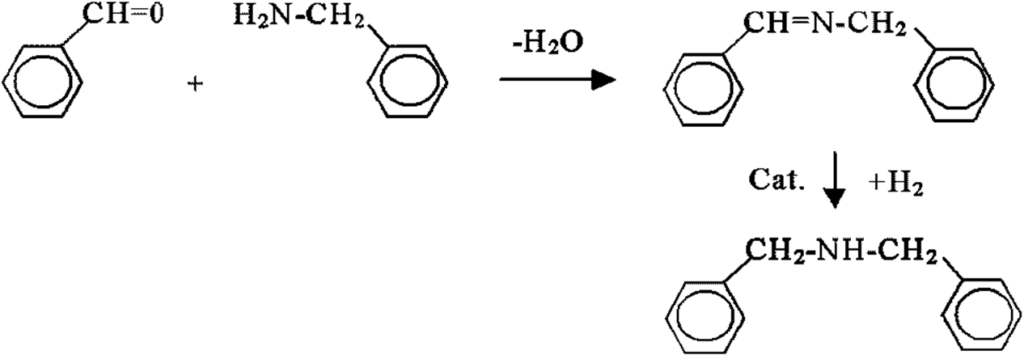
Meziprodukt typu Shiffovy vzniká spontánně oddělením vodné fáze, která ale působí katastrofálně nízký výtěžek (60%) konečného produktu. Pokud se ale před vlastní hydrogenací voda odeženeme, výtěžek vzroste na 98%. Zobecnění tohoto pozorování je, že je nutno zabránit vytvoření dvou kapalných fází, fáze organické a fáze vodné.
Porézní struktura katalyzátoru, zvláště na nosiči aktivní uhlí, vykazuje zpravidla obrovskou afinitu pro vodu. I malé množství vody může pak zvlhčit zrna katalyzátoru, ztížit přístup nepolárnímu reaktantu a v případě práškového katalyzátoru, aglomerovat jeho částice. To všechno pak zkreslí kinetiku, sníží rychlost žádoucí reakce a vyvolá nežádoucí boční reakce.
Dalším problémem může být usazování práškového katalyzátoru na dně reakční nádoby. Ukážeme si to na příkladu malého laboratorního autoklávu s centrálně umístěným míchadlem.
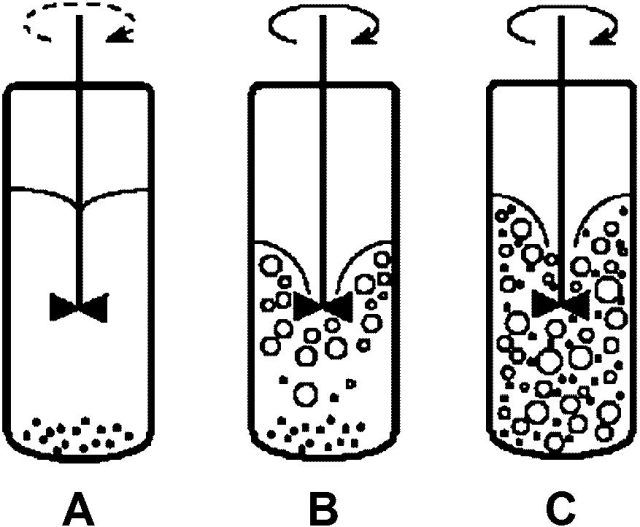
I v dobře homogenní reakční směsi je ale hlavním problémem zajištění dostatečného přísunu vodíku. Na tuto problematiku se nyní podíváme podrobněji.
Problém transportu vodíku
Hydrogenace je reakcí nenasyceného substrátu s vodíkem, který je takřka vždy deficitní komponentou. Je to dáno jeho velmi nízkou rozpustností v kapalné fázi. Rozpustnost vodíku činí (za normálního tlaku 1 atm a teploty 25°C), v ml plynného vodíku na mililitr rozpustidla: v metanolu 0,095, v etanolu 0,076, v cyklohexanu 0,092, v benzenu 0,071. Při hydrogenaci za normálního tlaku je tedy nutno dostat do roztoku každou minutu řádově 0,5 ml vodíku na 1 ml roztoku, jinak řečeno, obnovit veškerý vodík v reakční směsi zhruba 5 krát za minutu.
Následující obrázek dává první náhled problematiky transportu vodíku:
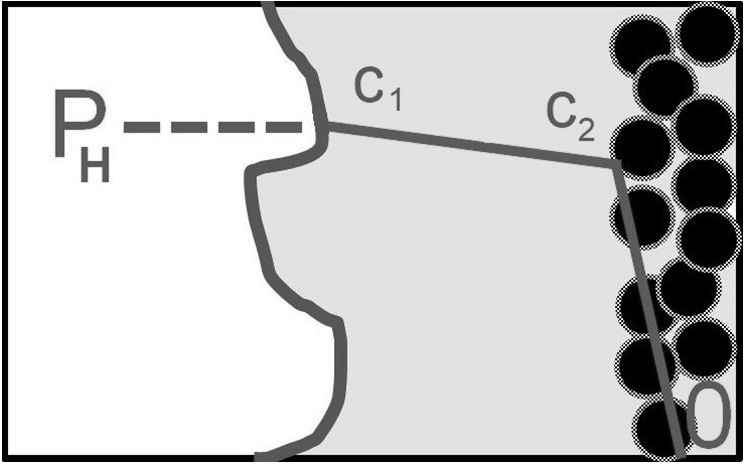
Vodík, jehož parciální tlak v plynné fázi je PH, prochází přes rozhraní plyn/kapalina. Kapalina na rozhraní se ihned nasytí vodíkem podle Henryho zákona,
c1= PH/H
kde H je Henryho konstanta. Poté vodík putuje kapalnou fází k laminárnímu filmu u povrchu katalyzátoru, kde je jeho koncentrace c2. Přes laminární film se dostává k vlastnímu povrchu, kde je jeho koncentrace cS; s touto koncentrací vstupuje do vlastního chemického děje. Z praktického hlediska je výhodné nahradit koncentrace v kapalné fázi „parciálními tlaky“ v kapalné fázi dle vztahu
Pi=H∙ci [2.1]
Cesta vodíku k povrchu katalyzátoru se označuje jako vnější difuze. Dříve, než je vodík spotřebován na povrchu katalyzátoru prochází porézní strukturou částic katalyzátoru, což se označuje jako vnitřní difuze; té se nyní budeme věnovat.
Analogie mezi elektrickou vodivostí, přenosem tepla a přenosem hmoty
Pro diskuzi jevů transportu hmoty a tepla je užitečné definovat analogii mezi těmito jevy a elektrickou vodivostí. Umožní nám to pak používat pojmy jako odpor či kapacita a jejich grafické symboly, jakož i zákony, platné pro síť odporů a kapacit.
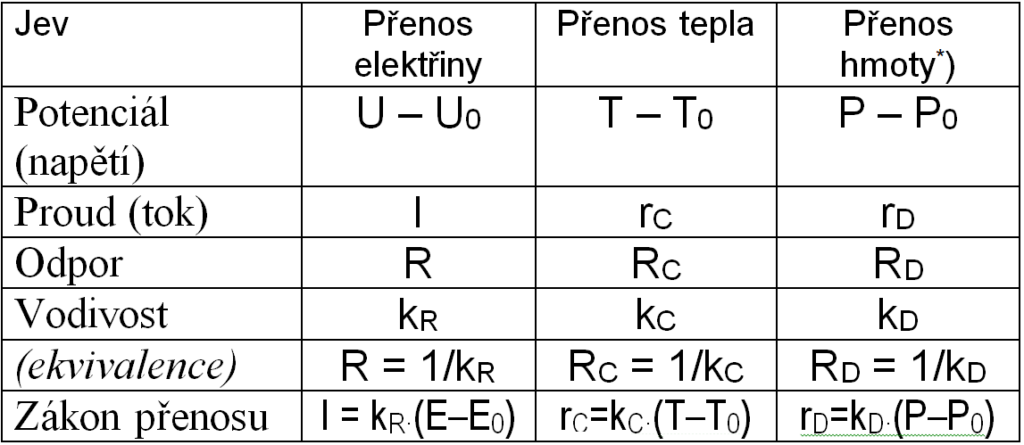
Tabulka 2.1: Analogie přenosu elektřiny, tepla a hmoty
Vnitřní difuze
Předchozí tabulka nám umožní vyjadřovat vnitřní difuzi vodíku v pórech katalyzátoru odporem proti přenosu hmoty, RD, přičemž rychlost transportu hmoty je dána vztahem rD=1/RD∙(P2-PS), kde PS je koncentrace vodíku u katalytického povrchu. Pro vlastní chemickou reakci, pokud je prvního řádu vůči vodíku, lze psát
r = k∙PS = (1/RV)∙PS [2.2]
kde
r lokální rychlost hydrogenace
PS aktivita vodíku u katalytického povrchu
RV Převrácená hodnota rychlostní konstanty
Symboly odporů RV a RD nám umožní vizualizovat problém vnitřní difuze následujícím způsobem:
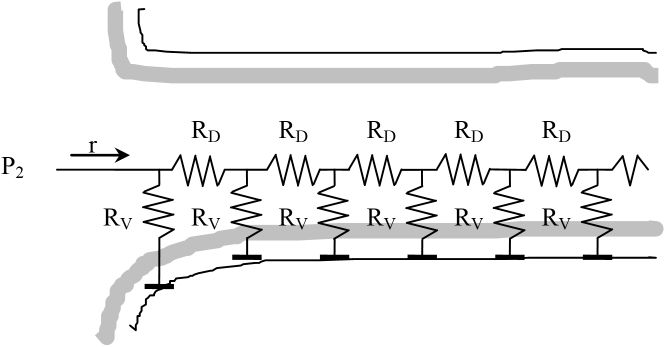
Je zde zobrazeno, jak vodík postupuje dovnitř póru, přičemž je současně spotřebováván chemickou reakcí. Celá tato soustava odporů může být vyjádřena jediným odporem R, jak ukazuje následující obrázek vlevo. Jedná-li se o nekonečnou síť odporů, pak celkový odpor R se nemůže změnit, pokud na počátku sítě přidáme ještě jednu dvojici odporů RV, RD (vpravo).
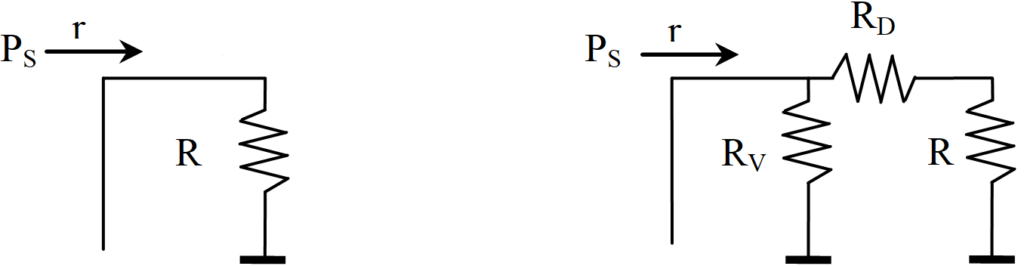
Ve smyslu Ohmova zákona lze psát
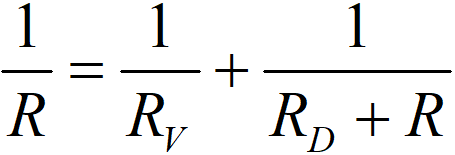
což dá
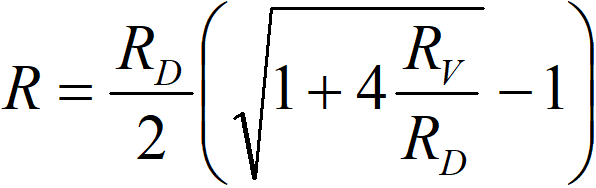
či pokud přejdeme k vodivostem,
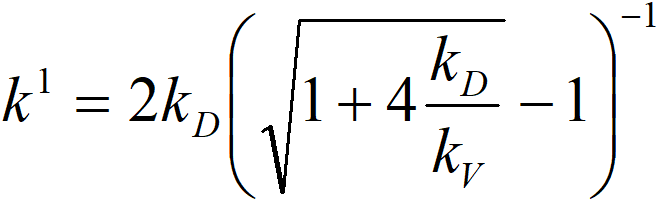
k1 pozorovaná rychlostní konstanta
kV rychlostní konstanta chemické reakce
kD difusní konstanta
Již z formy této rovnice můžeme soudit, že kvantifikovat vliv vnitřní difuze bude velmi obtížné – a to se zde jedná o ten nejjednodušší případ, totiž chemickou reakci 1. řádu k vodíku. Je tedy vhodné provádět pokusy za různých teplot a tím určit zdánlivou aktivační energii. Aktivační energie chemických reakcí (teplotní závislost konstanty kV) je řádově 10 kcal/mol, zatímco aktivační energie difuzních pochodů (kD) je řádově 2 kcal/mol. Hodnota někde uprostřed tohoto intervalu indikuje problém s vnitřní difuzí.
Při kinetických měřeních nezbývá než přijmout praktická opatření: rozdrtit katalyzátor na co možno nejmenší částice a ty pak udržovat homogenně rozptýlené v celém objemu reakční směsi. Vzpomeňme zde katalyzátor kdysi velmi populární, platinovou čerň… jehož objemová hmotnost je 21 g/cm³. Takový katalyzátor nezůstane rozptýlen, vždy se shromažďuje u dna reakční nádoby. Na trhu je naštěstí pestrý výběr katalyzátorů o mnohem nižší objemové hmotnosti, katalyzátorů nosičových. Tvoří je jemný a porézní prášek aktivního uhlí, křemeliny nebo aluminy, impregnovaných omezeným množstvím (1 – 5 %) aktivního kovu jako je platina, palladium, rhodium či jiné.
Vnější difuze
Vlastní kinetika hydrogenace, nazývaná „mikro kinetika“ je založena na termínu „aktivita vodíku u povrchu katalyzátoru.“ Vodík k povrchu katalyzátoru musí být dodáván transportem hmoty, aby pak byl spotřebován vlastní chemickou reakcí. Pokud označíme koncentraci vodíku u povrchu katalyzátoru cS a jeho rozpustnost v reakční směsi jako cH0, pak rychlost transportu hmoty, RD, je dána Fickovým zákonem,
rD = nD·(cH0 – cS) [2.6]
Jelikož rozpustnost vodíku v reakční směsi je přímo úměrná parciálnímu tlaku vodíku v plynné fázi reaktoru, PH, lze tuto reakci psát
rD = kD·(PH – PS) [2.7]
kde
PH Parciální tlak vodíku v plynné fázi,
PS Efektivní tlak vodíku u povrchu katalyzátoru,
kD——Celkový koeficient transportu hmoty.
Komplexní konstanta kD zahrnuje:
- Rozpustnost vodíku v reakční směsi (a její závislost na teplotě.) Vyjadřuje se Henryho konstantou H:
cH0 = PH/H cS = PS/H
- Difuzní koeficient (a jeho teplotní závislost)
- Objem kapalné fáze
- Množství bublinek plynného vodíku v reakčním prostředí a obecně, intenzitu míchání kapalné fáze
Rychlost vlastní chemické reakce, r, dá se psát jako
r = W·k(T)·f(PS,c,…) [2.8]
kde
W množství katalyzátoru
k rychlostní konstanta, jež zahrnuje
- teplotní závislost (Arrheniův zákon)
- vlastní aktivitu katalyzátoru
- konstantu úměrnosti
f(PS,c…) jistá funkce, závislost na
- parciálním tlaku vodíku u povrchu katalyzátoru (PS),
- koncentraci hydrogenované látky (c),
- koncentraci dalších složek reakční směsi
Za podmínek ustáleného stavu (což určitě platí vzhledem k nízké rozpustnosti vodíku),
r = rD [2.9]
Tato rovnice otevírá cestu k určení koncentrace vodíku u katalytického povrchu, PS. Pokud do reakční směsi přidáme opravdu nadměrnou dávku katalyzátoru, pak se dá předpokládat, že r >> rD a PS → 0. Rovnice reálné rychlosti pak je
r = kD·PH [2.10]
kde
r reálná rychlost hydrogenace, ovlivněná difuzí
kD difuzní konstanta
PH parciální tlak vodíku v plynné fázi
Tímto způsobem, tedy hydrogenací s velkým nadbytkem katalyzátoru je možno stanovit difuzní konstantu a ta pak poslouží ke korekci vlivu transportu hmoty v kinetických měřeních s běžnou dávkou katalyzátoru. Později si ukážeme praktický příklad.
Autokláv pro hydrogenaci za zvýšeného tlaku
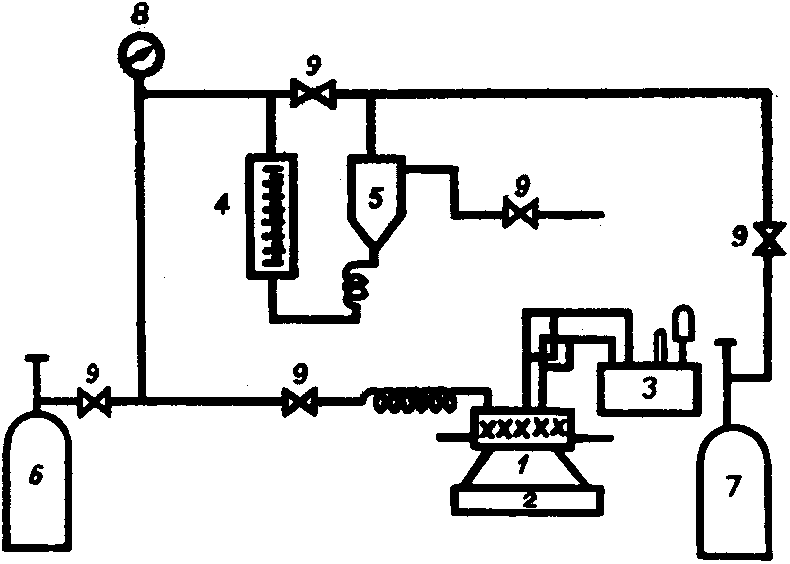
Na obrázku 2.1 jsme již zobrazili zjednodušený model reaktoru pro heterogenní hydrogenaci. Příklad skutečné instalace je na následujícím obrázku.

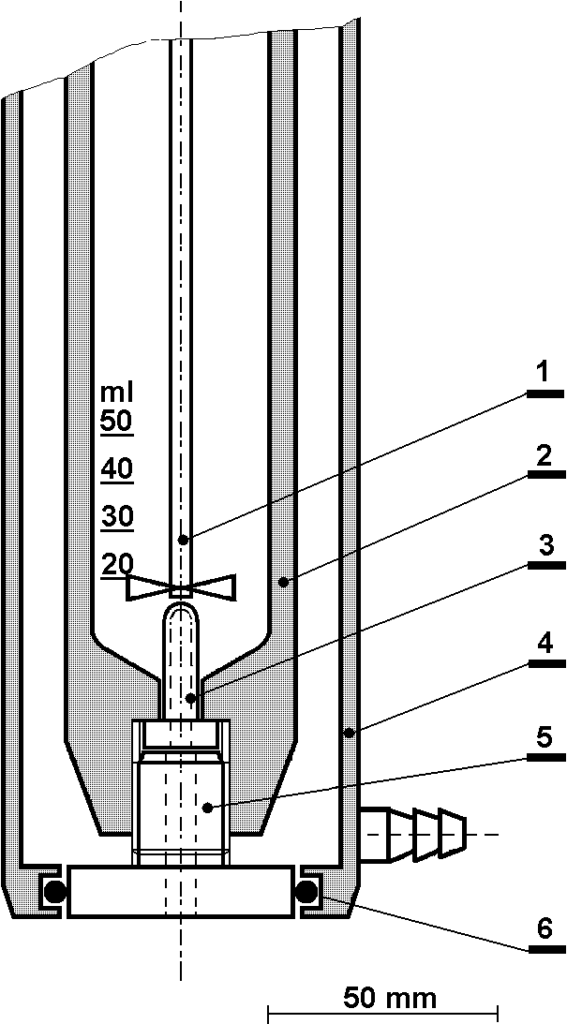
Tento autokláv je vybaven dvojím pláštěm pro cirkulaci chladiva. Nádoba autoklávu je míchána axiálním míchadlem s magnetickou hlavou, poháněnou pohonem mimo tlakový prostor. Vodík je přiváděn z tlakové nádoby přes regulátor tlaku a přes ventil. Fotografie je stará téměř 50 let, dnes se pro záznam teploty použije DVM a numerický zapisovač.
Nádoba našeho autoklávu o objemu 200 ml je úzká a vysoká, což je nepříznivé pro homogenizaci reakční směsi. Je třeba zkoušet různé objemy kapalné fáze a různé otáčky míchadla. Je nutno především docílit protržení hladiny kapaliny pro nasycení objemu bublinkami plynu – rozpouštění vodíku pouze přes hladinu kapaliny by bylo absolutně nedostatečné. Další nezbytností je homogenizovat reakční směs z hlediska katalyzátoru, aby se částice katalyzátoru neshromažďovaly u dna, viz obrázek 2.1. Experimentálně zjištěný vliv množství kapalné fáze a otáček míchadla je na obr 2.6.
Kinetická studie:
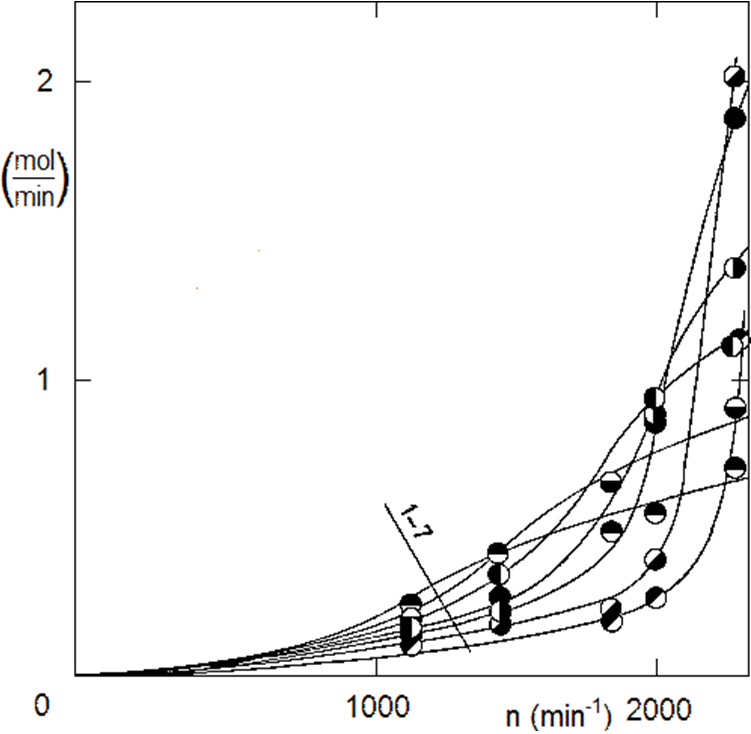
Při nadměrné dávce katalyzátoru konstatujeme při zvyšování otáček míchadla obrovský nárůst spotřeby vodíku. Je tedy evidentní, že je třeba zvýšit otáčky míchadla na maximum. Směs je třeba přímo šlehat, aby vznikla opravdová pěna. Průmyslové autoklávy k tomu používají různá opatření, kupříkladu, vodík se přivádí vždy přímo pod míchadlo – ať už přes dutou osu míchadla, nebo boční přívodní trubkou. Gazifikaci průmyslových autoklávu napomáhají i vestavby v nádobě autoklávu, kupříkladu chladicí had. Když se vrátíme k laboratornímu autoklávu: nemějte strach zvyšovat otáčky míchadla z obav o životnost ložisek osy míchadla. Ve skutečnosti totiž rotující hmota sestavy míchadla s magnetickou hlavou stabilizuje osu míchadla, tak jako dětská káča. Právě při nižších otáčkách se projevuje boční házení, což snižuje životnost uložení. V sestavě na obrázku 2.4 byl původní pohon s motorem a řemenicí (se kterým byla realizována měření dle obr. 2.6) nahrazen mohutným asynchronním motorem s otáčkami 3000 min-1.
Sledování průběhu hydrogenace v kapalné fázi
Začneme zasloužilou katalytickou kačenou, obr. 2.7. Jedná se o skleněnou nádobku s dvojí stěnou, plášť (zde v řezu) je temperován proudem kapaliny – přenašeče tepla. Kačena je upevněna na třepačce. Tohle zařízení vypadá zastarale, ale může být stále velice užitečné, třeba už proto, že je skleněné a tedy pokud se dovnitř nainstalují elektrody, je možno pozorovat zajímavé věci.
Reaktor je připojen na systém byret (zde napravo jsou ve zmenšeném měřítku), byrety slouží k měření množství spotřebovaného vodíku.
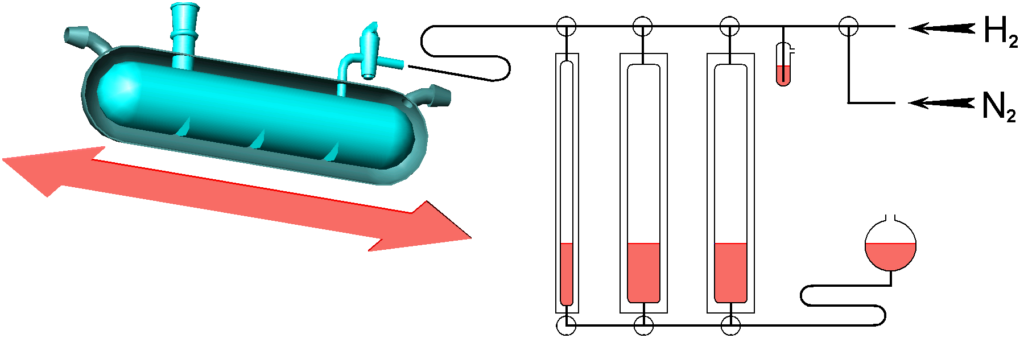
Hladina kapaliny v byretách se ustavuje ručně pomocí pohyblivé vyrovnávací nádobky. To, že se vodík sytí tenzí vyrovnávací kapaliny, může být problém. Existují nicméně i „suché“ varianty s válcem a pístem.
Před mnoha lety několik sovětských laboratoří zkoušeli stejný systém, samozřejmě z oceli a s pancéřovými byretami, pro tlaky až de 10 MPa (100 atm) – obr. 2.8. Podle našeho názoru museli mít problém s udržováním teploty. Pokud se totiž kupříkladu za tlaku 10 MPa změní teplota 400 K na 402 K, tlak v systému se změní (T1/T2 = P2/P1) o 0,5 %, což představuje 5m vodního sloupce na byretě… Nepoužívat!
Přejděme nyní k průmyslovým instalacím. Pro měření průtoku vodíku do autoklávu jsou dostupné průtokoměry, jsou ale drahé, s nedostatečným rozsahem a nepříliš spolehlivé. Jediný rozumný systém spočívá v instalaci uzavíracího ventilu na přívodu vodíku, který se otevírá jen dočasně v situaci, kdy tlak v systému klesne na určitou mez, kupříkladu o 10 %. Na obrazovkách řídicího systému pak lze sledovat průběh hydrogenace. Záznam vypadá nějak takto:
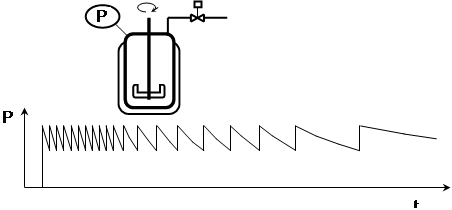
Při tomto způsobu řízení lze dobře odhadnut, kdy je třeba šarži ukončit; včasné ukončení je dobré pro selektivitu i pro ekonomiku. Jednoduchý řídicí systém má i další funkce, především havarijního odstavení uzavřením přívodu vodíku – při nedostatku vodíku se reakce přirozeně zastaví.
Varianta: U jednoho komerčního autoklávu je popsáno měření průtoku přes vyrovnávací nádobku, vybavenou manometrem a dvěma uzavíracími ventily: během střídavého otevírání ventilů lze z poklesu tlaku ve vyrovnávací nádobce známého objemu spočíst množství přivedeného vodíku (obr. 2.10.)
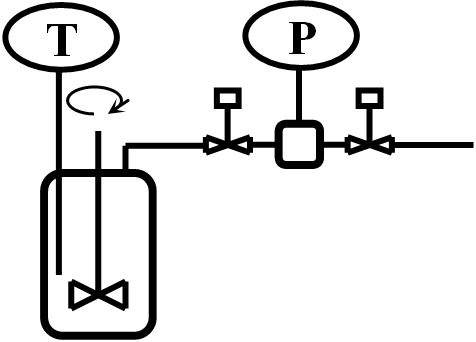
Ještě k průmyslové praxi: v literatuře se občas doporučuje vést hydrogenaci při omezeném míchání. V takovém režimu zdánlivá aktivační energie klesá a systém se snáze kontroluje. Z ekonomického hlediska nemá ale smysl používat drahý vysokotlaký autokláv, je-li možno pracovat v lacinějším autoklávu za nižšího tlaku, ale s účinnějším mícháním. Navíc obecně platí, že každé prodlužování trvání šarže ohrožuje selektivitu procesu, snižuje výtěžek.
Pro laboratorní kinetická měření není volumetrické sledování ideální. Již samotné změny tlaku jsou pro kinetická měření nevhodné, vadí hlavně, že při každém dopouštění vodíku se teplota reakční směsi skokově změní o několik desetin stupně (Joule–Thomsonův efekt), což samozřejmě kinetická měření znehodnocuje.
Sledování tepelnou bilancí
Exotermní reakce, jako je hydrogenace, jsou doprovázeny uvolňováním tepla. K odvodu tohoto tepla se musí vytvořit jistý teplotní spád. Tento teplotní spád je úměrný množství uvolněného tepla a tedy rychlosti hydrogenace. Pokud se nám podaří tento fenomén popsat, získáme velmi přirozený prostředek sledování chemické reakce.
Bilance tepla i teplotní pole v systému autoklávu jsou velmi komplikované. Vždyť kupříkladu jenom tepelná kapacita ocelového pláště autoklávu je srovnatelná s tepelnou kapacitou samotné reakční směsi.
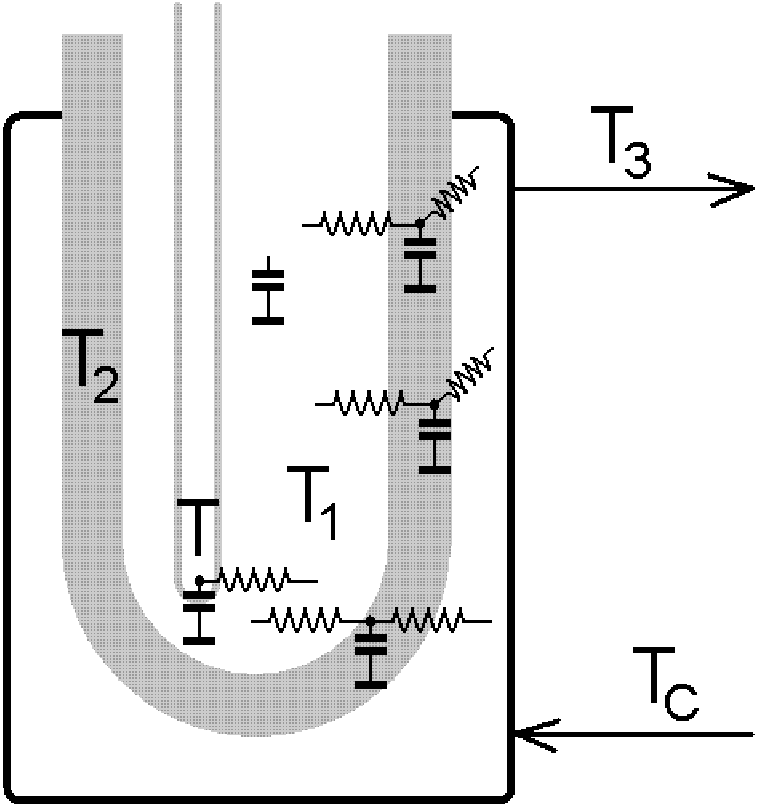
Jak ukazuje náš obrázek, přenos tepla se děje přes nekonečnou síť kapacit a odporů. Přesto je možno přikročit ke zjednodušením, například brát teploty T a T1 jako identické a předpokládat, že teplota T2 je mnohem bližší teplotě T1 nežli teplotě T3, jinak řečeno, že odpor proti přenosu tepla je soustředěn na rozhraní mezi nádobou autoklávu a přenašečem tepla. Pak je možno se pokusit o nahrazení celého systému jedinou kapacitou a jediným odporem,
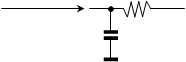
a vytvořit extenzivní bilanci tepla, tj. bilanci, jež zahrnuje celý reakční systém a celý autokláv:
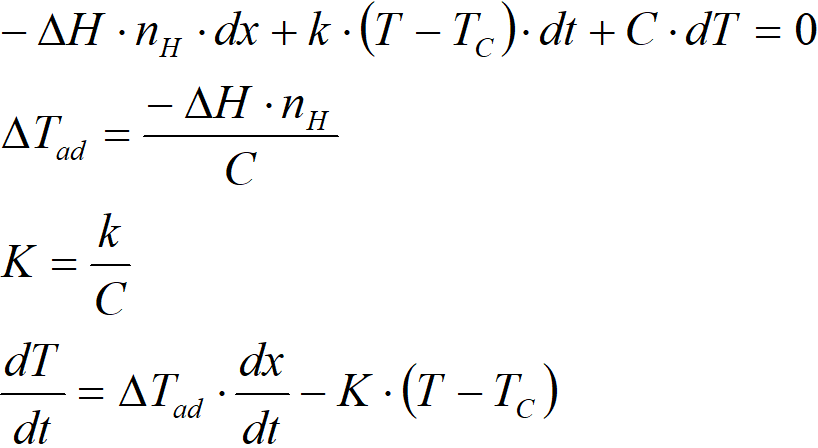
kde
∆H molární entalpie reakce, kJ∙mol-1
nH celkováspotřebavodíku, mol
x konverze
k Celkový koeficient přenosu tepla, kJ∙K-1∙s-1
T teplota reakční směsi, K
TC teplota přenašeče tepla, K
t čas, s
C tepelná kapacita systému, kJ∙K-1
∆Tad adiabatický teplotní rozdíl, K
K chladicí konstanta reaktoru, s-1
kcelkový koeficient přenosu tepla, kJ∙K-1∙s-1
Pro grafickou presentaci je výhodné ještě nadefinovat parametr „S“, s rozměrem K∙s∙mol-1
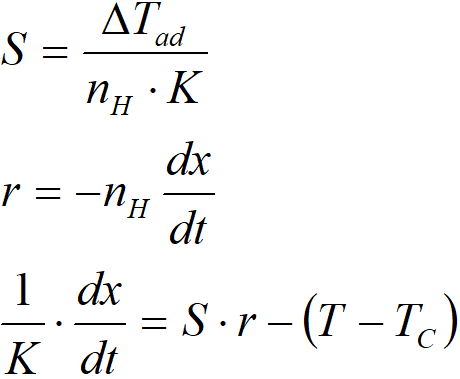
Pokud je dx/dt =0, pak rovnice nabývá tvaru: S·r = T–TC. Součin S·r tedy vyjadřuje ustálený rozdíl teplot, pokud by reakce probíhala dostatečně dlouhou dobu konstantní rychlostí.
Tepelná bilance [2.12] zahrnuje dvě konstanty, K a ∆Tad. Tyto dvě konstanty nejsou navzájem nezávislé, jsou spojeny přes integrál tepelné bilance,
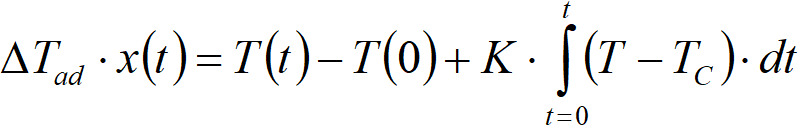
kde
x(t) konečná konverze
T(t) konečná teplota
T(0) počáteční teplota (pro x=0)
Je tedy možno vyčíslit konstantu ∆Tad na základě hodnoty K. Hodnotu K je možno experimentálně odhadnout prostým pokusem, kdy necháme temperovat reakční směs bez katalyzátoru (r=0), tedy
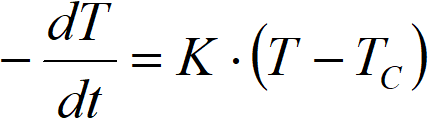
Výchozí teplotní gradient vytvoříme kupříkladu vhozením kousku suchého ledu (CO2) do roztoku v autoklávu a pak zapisujeme teplotní odezvu.
Náš model nyní ověříme hydrogenačními pokusy. Obrázek 2.12 (viz níže) porovnává konverze vypočtené tímto modelem s analýzami GLC hydrogenací, ukončených při různých konverzích.
Srovnání potvrzuje vhodnost metody. Dokonce pokud použijeme značně nepřesnou hodnotu K (správná hodnota pro otáčky míchadla 2500 min-1 je 1,8 min-1), i pak jsou vypočtené křivky velmi blízko výsledkům přímé analýzy GLC. Je ovšem pravda, že daná reakce probíhá prakticky konstantní rychlostí; rychlosti vypočtené na počátku pokusu a k jeho konci, kdy jsou změny teploty významnější, jsou méně přesvědčivé (viz například obrázek 2.14 níže).
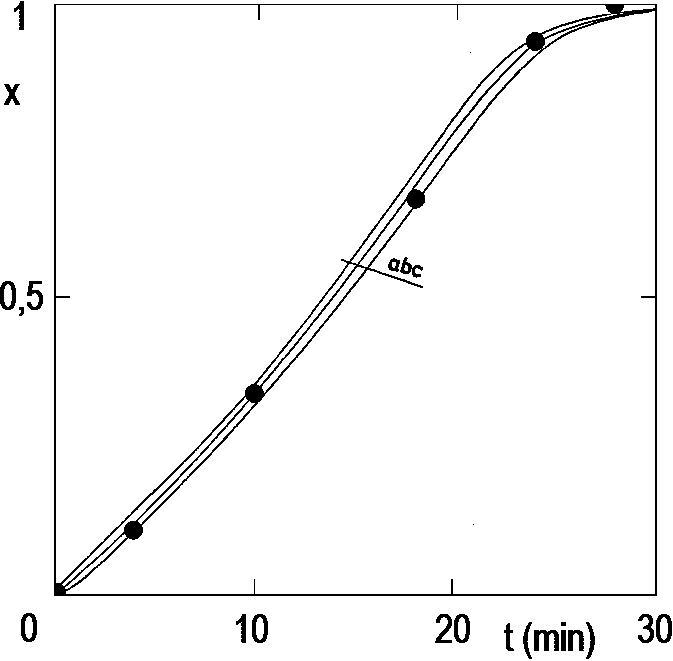
Konstatujeme tedy, že tepelná bilance představuje jednoduchou a účinnou analytickou metodu. Měli jsme pouze ten problém, že teplotní diferenci jsme měřili termočlánky, jež dávají řádově jen 50 µV/K; proto nelze ani s nejmodernějšími voltmetry měřit přesněji než na 0,1 K. Na trhu jsou nyní ovšem snímače Pt100 v miniaturním provedení a tyto ve spojení s běžnými systémy sběru dat (třeba: YET-720L) měří 100 krát přesněji.
Na obrázku 2.13 je zobrazeno několik rychlostních křivek, naměřených při různých tlacích vodíku.
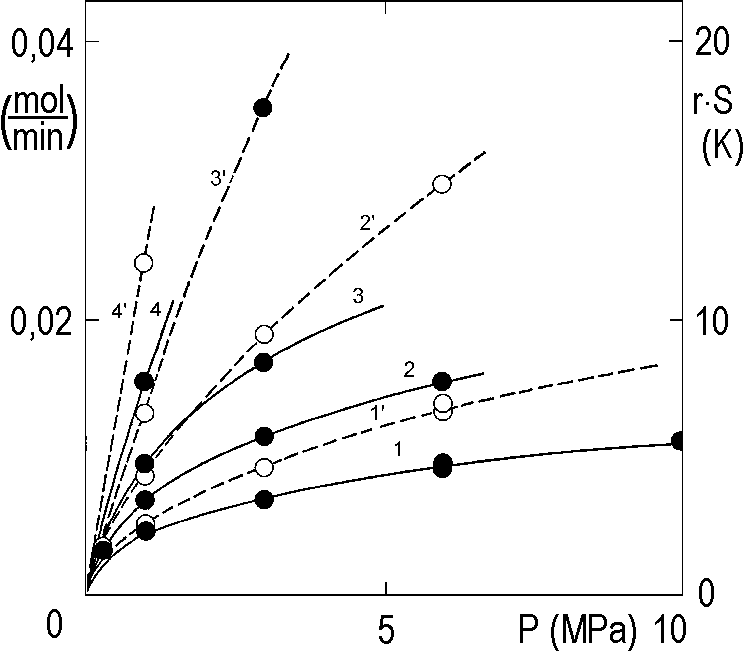
Na svislé ose vpravo je na tomto obrázku vynášen součin r·S, což poskytuje obraz o ohřevu reakční směsi během pokusu. Uvolněné teplo zvyšuje teplotu, za jistých podmínek, až téměř o 20 K. Platí přitom rámcové pravidlo, že zvýšení teploty o každých 10 K zdvojnásobuje rychlost. Křivky vynesené na obrázku 2.13 čárkovaně tedy nenabízejí žádnou představu o kinetice za konstantní teploty.
V dalším odstavci navrhneme metodu korigování dat, zatížených vlivem vnějšího přenosu hmoty a tepla. Výstupem jsou pak izotermní kinetická data. Metoda není úplně univerzální, má ale tu přednost, že je velmi instruktivní.
Postup eliminace vnějších přenosů hmoty a tepla
Experimentální data, jež budeme dále zpracovávat, jsou extenzivní (vztažené na celý systém) a proto je nutno dodržovat neměnný objem reakční směsi a neměnné vnější parametry v celé sérii pokusů. Jedná se o studii hydrogenace nitrobenzenu (10 ml nitrobenzenu ve 30 ml etanolu) na katalyzátoru 3 % Pd/C (100 mg) za zvýšeného tlaku vodíku a to za podmínek, kdy vnější přenost tepla a hmoty nejsou zanedbatelné. Začneme rovnicí [2.7] (viz výše),
rD = kD·(P – PS) [2.7]
Pro zjištění hodnoty celkového koeficienty transportu vodíku kD provedeme sérii měření za relativně nízkého tlaku a s velkým nadbytkem katalyzátoru.
Obrázek 2.14 ukazuje průběh několika pokusů se zvýšeným množstvím katalyzátoru. Konverzní křivky byly vypočteny z křivek teplotních již popsaným postupem – nevšímejte si jejich průběhu za příliš nízkých nebo příliš vysokých konverzí, v těchto oblastech numerická derivace selhává z důvodu prudkých změn teploty. Pozorujeme zde, že při relativně nízké dávce katalyzátoru, tedy v kinetických podmínkách, je reakce prakticky 0. řádu vůči hydrogenované látce. Je tu ale zajímavý paradox, při nadměrných dávkách katalyzátoru, tedy v difuzních podmínkách rychlost s konverzí poněkud klesá. Zde se projevuje změna rozpustnosti vodíku v reakční směsi s pokračující konverzí (Pi=H∙ci, přičemž jak se zde ukazuje, Henryho konstanta závisí na složení reakční směsi). Plné body ukazují rozpustnosti vodíku naměřené nezávislou metodou v modelových směsích, ale za nižší teploty.
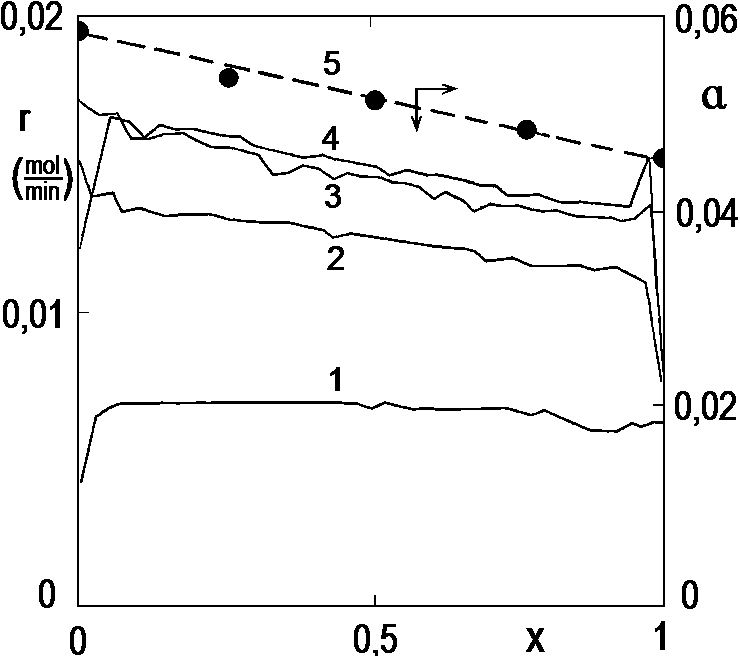
Plné čáry – rychlost hydrogenace (r) v závislosti na konverzi při 40 °C, 0,29 MPa. Množství katalyzátoru (g): 1 – 0,1; 2 – 0,3; 3 – 0,7; 4 – 1,2.
V následujícím budeme diskutovat pouze rychlosti při konverzi x=0,5. Na obrázku 2.15 jsou pokusy z obrázku 2.14 plus výsledky dalších měření.
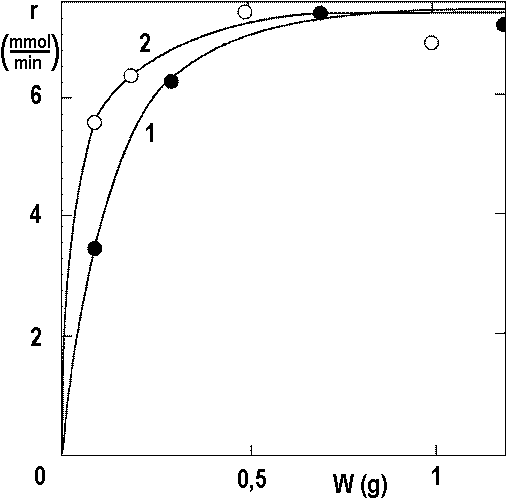
Teplota TC: ●1 – 40 °C, ○2 – 70 °C.
Údaje z obrázku 2.15 umožní odhad hodnoty ND: pokud se PS → 0, dostáváme ND = RD/P.
Na obrázku 2.13 jsme zobrazili rychlost hydrogenace v závislosti na tlaku, ovšem naměřené křivky (prázdné body) byly ovlivněny vnějším přenosem hmoty a tepla do té míry, že neměly žádnou vypovídací schopnost. Je nezbytně třeba očistit je od vlivu transportních jevů. Znovu opakujeme, že následující metoda není zdaleka univerzální, ale zato je velmi instruktivní.
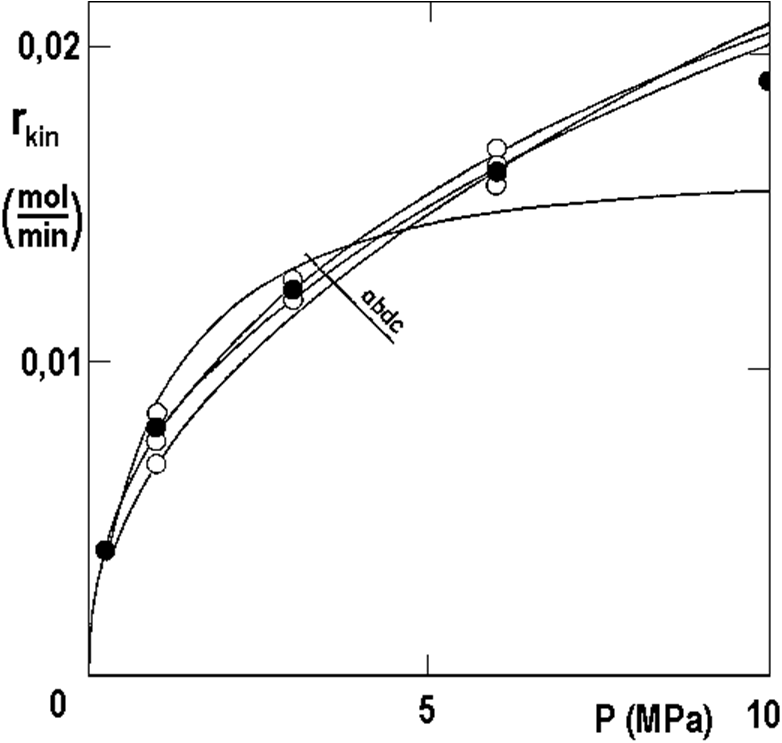
Korekce vyžaduje přijmout hypotézu o tvaru reakční rychlosti. Nejrozumnější je zvolit mocninovou závislost,
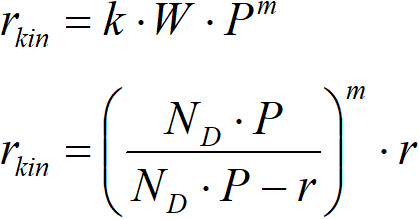
Tato rovnice je základem iteračního algoritmu, kdy se provede první odhad m a poté se získá první odhad hodnoty aktivační energie.
Následující obrázek 2.16 ukazuje, v Arrheniovských souřadnicích, dvě sady dat z obrázku 2.15 – vlevo naměřené hodnoty, vpravo korigované hodnoty. Křivky na levém obrázku nejsou rovnoběžné, zatímco přímky napravo, odhad na základě rovnice [2.16], jsou již téměř rovnoběžné.
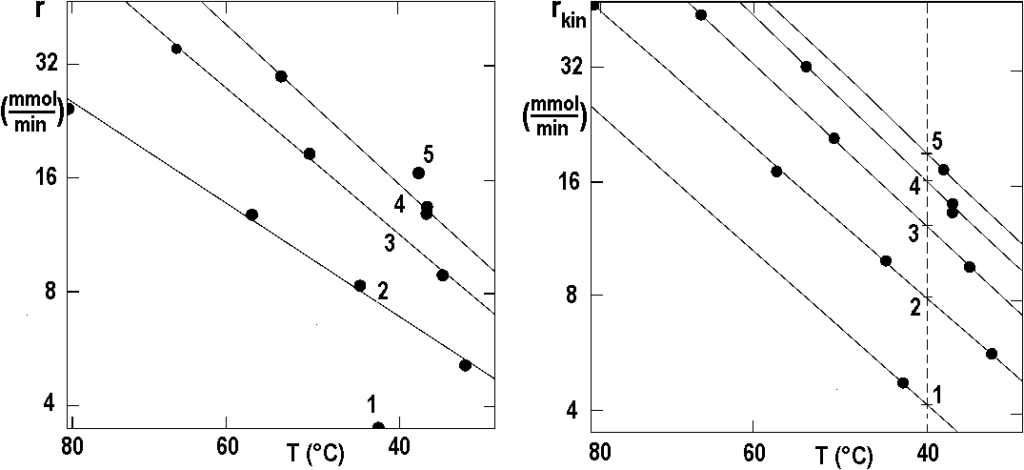
Izotermní body z obrázku 2.16 jsou zobrazeny na následujícím obrázku 2.17 v závislosti na tlaku v logaritmických souřadnicích. Směrnice spojnice činí 0,42 a s touto hodnotou je možno iteraci zopakovat.
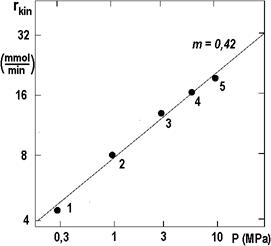
Výsledek všech těchto snažení byl již zobrazen na obrázku 2.13: jsou tam naměřené křivky (prázdné body, spojnice čárkovaně) a křivky korigované (plné body, nepřerušované čáry) pro teploty Tc, (°C): 1 – 30; 2 – 40; 3 – 50; 4 – 70.
Úprava výsledků „vážením“
Vzhledem k omezenému rozsahu měření je třeba seskupit všechny výsledky do jediné křivky. Teploty se přepočtou na jedinou teplotu, kupříkladu na T0 = 40 °C. Dále je dobré nedůvěřovat přehnaně bodům, které vyžadovaly velké korekce na transport hmoty. Je proto vhodné přikročit k určitému vážení,
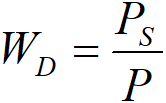
Obrázek 2.18 přebírá všechny body z obrázku 2.13, přepočtené na teplotu T0 = 40 °C (prázdné body). Tyto body byly podrobeny zprůměrování s váhami WD, což dalo plné body. Těmito body jsme metodou regrese proložili zkusmo křivky, odpovídající čtyřem různým modelům:
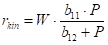
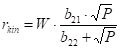
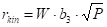
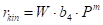
Každý model z obrázku 2.18 odpovídá nějaké představě o řídícím kroku hydrogenace, kupříkladu pro (a) je rychlost určována adsorpcí vodíku v molekulární formě H2, model (b) odpovídá představě o adsorpci vodíku v atomární formě H, (c) je totéž pro velmi nízké pokrytí povrchu, (d) je mocninová závislost pro m=0,42.
Interpretace experimentálních výsledků
Říká se, že pokud má model tři čtyři parametry, je už možno namodelovat slona. A tím končí mnohá diskuse…
Když se vrátíme k seriózním úvahám, tak obrázek 2.18 ukazuje, že je vždy možno interpolovat experimentální data nějakou křivkou, že ale není vždy možné rozhodnout který model je správný, pokud není k dispozici dostatečný objem experimentálních dat. V daném případě by bylo žádoucí měření při jednom ještě vyšším tlaku, ale k tomu jsme se tenkrát už nedostali …
Ještě obecně o reprodukovatelnosti měření při katalytické hydrogenaci. Pokud chcete dosáhnout série koherentních kinetických měření, je nutno měření věnovat zvláštní péči, jež se může jevit až přehnaná. Tak pro celou sérii pokusů je nutno používat vodík z jediné tlakové nádoby. Katalyzátoru si rezervujte nadbytečné množství a hlavně se vyhněte katalyzátoru čerstvě připravenému. Před použitím lahvičku s práškovým katalyzátorem dobře protřepat. Někdo trvá na hydrogenované látce čerstvě připravené, pokud ale budete látku k hydrogenaci destilovat každé ráno, nedocílíte nikdy koherentních výsledků hydrogenačních pokusů. Správný postup je zde destilovat jen jednou a uchovávat látku k hydrogenaci pod dusíkem v přesných dávkách (kupříkladu, 25 ml) v zatavených ampulích nebo v lahvičkách uzavřených teflonem. Při každém pokusu se do reaktoru nalije celý obsah lahvičky – dávkování lze kontrolovat diferenčním vážením plné a prázdné lahvičky. Problém vlhkosti již jsme zmínili; dá se mu předejít použitím polárního rozpouštědla, v pokusech probraných v předchozím se použilo 25% obj. nitrobenzenu v etanolu. Je nutná série předběžných pokusů pro dokonalé zvládnutí experimentální techniky. Tak nějak je tedy třeba postupovat, abychom docílili výsledků „prezentabilních“, jak říkají Francouzi.